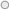![]()
Simplificación por el método gráfico de Karnaugh de funciones de más de 4 variables
Mapas K de 5 variables
En este caso, al ser 5 variables, se dispondrán de 2^5 = 32 casillas. Para hacer una representación del mapa correspondiente a las variables A,B,C,D y E se debe realizar un gráfico como el de la siguiente figura:
----------------------------------------------------------------
----------------------------------------------------------------
El resultado es un mapa de Karnaugh de 4 variables, el primero de ellos para A= 0 y el segundo para A=1. Las variables se han puesto en color azul y los valores numéricos de las casillas de color rojo.
Las variables se han ordenado de la forma ABCDE. Para comprobar esta circunstancia se puede observar que la casilla identificada ABCDE = 00001 (mapa de la izquierda, primera columna, segunda fila) tiene el valor decimal 1.
La aplicación del procedimiento es similar al de 4 variables aunque a la hora de encontrar casillas adyacentes, las casillas situadas en ambos mapas en la misma posición relativa se “tocan”. Es decir, es como si el mapa de la izquierda estuviera situado sobre el de la derecha de forma que las casillas BCDE=0000 de ambos mapas son adyacentes y así con el resto de casillas cuyos valores BCDE sean iguales.
Esto da lugar a una mayor posibilidad de combinaciones a la hora de realizar grupos (ahora tiene más sentido llamarlo cubos) y es necesario estar atento durante la realización del procedimiento.
----------------------------------------------------------------
----------------------------------------------------------------
Mapas K de 6 variables
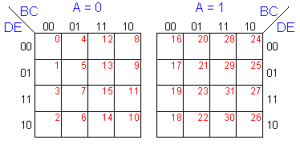
El mapa K de 6 variables es una nueva extensión del de 4 variables, aunque ahora es necesario alojar a 2^6 = 64 casillas. En la figura siguiente se puede observar una representación cuando las variables son ABCDEF:
----------------------------------------------------------------
----------------------------------------------------------------
Ahora, las variables A y B son las que se utilizan para identificar cada uno de los 4 mapas K de 4 variables.
El procedimiento de obtención de grupos (o cubos) es, en concepto, el mismo que para los casos anteriores. Sin embargo, la búsqueda de adyacencias para formar los grupos debe extenderse a las casillas equivalente de los mapas de la izquierda (o derecha) y de arriba (o abajo). Esto incrementa la dificultad de realizar el procedimiento correctamente.
Mapas de más de 6 variables
A la vista de los expuesto en estos apartados, se puede extrapolar en teoría el método a cualquier número de variables duplicando cada vez el número de mapas K de 4 variables.
Se puede constatar, sin embargo, que la dificultad de formar grupos hace que la probabilidad de cometer errores aumente significativamente con el número de variables consideradas. Esto hace que sea desaconsejable el uso de este método para muchas variables y se utilice otra alternativa.
----------------------------------------------------------------
----------------------------------------------------------------