¿Qué es la Lógica Difusa o Fuzzy Logic?
La conocida como Fuzzy Logic es la lógica que utiliza expresiones que no son ni completamente ciertas ni falsas. Es una lógica difusa. Actualmente, es una de las disciplinas matemáticas con un mayor número de seguidores.
La Fuzzy Logic se aplica a conceptos que pueden adquirir un valor cualquiera de veracidad dentro de un conjunto de valores que oscilan entre dos extremos:
- La verdad absoluta
- La falsedad total
Es importante tener en cuenta que lo difuso no es la lógica en sí, sino el objeto que se estudia. Esto se debe a la falta de definición del concepto al que se aplica. La Fuzzy Logic nos permite jugar con información que no es precisa. Por ejemplo, «temperatura baja» o «estatura media», en términos de conjuntos que no son claros.
Este tipo de lógica surge de la necesidad de utilizar en nuestra vida diaria esos adjetivos del lenguaje natural con los cuales estamos cualificando y, de esta manera, poder volcarlos o cuantificarlos de alguna forma. Esta cuantificación de los adjetivos será la base que vamos a intentar tratar mediante la Fuzzy Logic.
¿Cómo surge la Fuzzy Logic?
La Fuzzy Logic nació de la mano de Lofti A. Zadeh, un iraní de nacionalidad americana, matemático y catedrático de la Universidad de Berkeley de California. El autor sintió la necesidad de aportar en el campo de la matemática una nueva lógica multievaluada. Esto significa que va más allá de la lógica booleana.
Zadeh presentó la fuzzy logic como una forma de procesamiento de la información en la que los datos podrían tener asociados un grado de pertenencia parcial a conjuntos. Hacia 1970 se empezó a aplicar esta teoría en los sistemas de control y, desde entonces, el número de aplicaciones industriales y su ejecución ha aumentado exponencialmente.
Mediante esta lógica el autor quería facilitar la expresión mediante las etiquetas del lenguaje natural y poder acercarnos más a ese tratamiento natural del lenguaje a la hora de intentar cualificar y cuantificar dentro de lo que es el desarrollo de sistemas de información.
¿Para qué sirve la Fuzzy Logic?
Se trata de una disciplina que nos permite tratar información imprecisa. Veamos un ejemplo. La temperatura se puede medir en grados centígrados. Es decir, podemos decir que hace 16 grados y medio, pero también la podemos medir de una forma no precisa. Por ejemplo, como «hace frío», «hace un poco de frío» o «hace un poco de calor». Dicho esto, tenemos que establecer qué valores son los que abarcan frío, calor, etc.
Aquí es donde entra la fuzzy logic, ya que nos permite moderar este tipo de información. Esta lógica parte de la teoría clásica de conjuntos. Esta teoría dice que un elemento puede pertenecer o no a un conjunto. Pero la fuzzy logic nos permite establecer rangos de pertenencia más allá del 0 y 1.
Es decir, en vez de decir «esto es frío» o «esto es cálido», pues podemos decir: «esto es 0,5 unidades de frío» o «0,8 unidades de cálido». Esto es lo que nos permite moderar frases del estilo «hace un poco de frío» o «eres alto».
La pertenencia de un elemento a un conjunto borroso se calcula mediante su función de pertenencia, que es una función a trozos que determina el grado de pertenencia en función de intervalos. Otro de los elementos que conforman los conjuntos borrosos son las particiones borrosas. También tenemos que definir el conjunto de partición borrosa, que es un conjunto de conjuntos borrosos. Concretamente, es un conjunto de todos los conjuntos que se han definido para una determinada variable.
Sigamos con el mismo ejemplo. Para la variable «temperatura» podríamos tener tres conjuntos borrosos. Estos serían «cálido», «templado» y «frío». Una partición borrosa sería el conjunto de las tres. Estos conjuntos se relacionan en funciones de pertenencia. Las formas más típicas para estas funciones son la trapezoidal, la triangular y la singleton.
Por último, hay que definir la variable lingüística. Esta variable es aquella que toma valores que son términos del lenguaje natural como poco, mucho o bastante. Estas variable sirven como etiquetas para el conjunto borroso.
Aplicaciones de la Fuzzy Logic
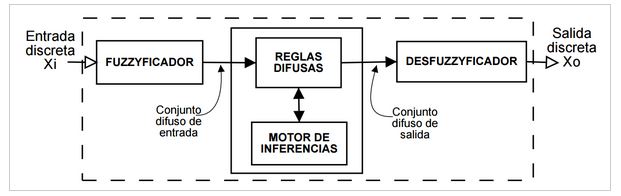
Las aplicaciones de la Fuzzy Logic podemos ampliarlas a los sistemas expertos o podemos desarrollar controladores borrosos. Algún ejemplo de controlador borroso sería el controlador de un termostato. Lo primero que tenemos que tener en cuenta para definir un controlador borroso es que hay que definir las particiones. Generalmente, estas particiones tienen que ser completas. Es decir, tienen que cubrir todo el rango de valores posible para el problema que pretendemos resolver.
Por otro lado, también es habitual definir un solapamiento entre variables de entre un 20% o un 30%. En el ejemplo de las temperaturas, este solapamiento se encontraría, por ejemplo, en los 19 grados. Los 19 grados pueden ser una temperatura templada pero también podrían acercarse a ser una temperatura cálida.
También es importante definir las reglas borrosas, que nos permiten unir los conjuntos borrosos de entrada con los conjuntos borrosos de salida.
Lógica difusa - Wikipedia, la enciclopedia libre
Introducción a la Lógica Difusa
Fuentes:
- iebschool
- wikipedia
- cs.us.es