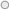![]()
Circuitos RLC en paralelo y mixtos en corriente alterna.
Es muy importante para poder entender los circuitos con receptores en paralelo y mixtos.
En las instalaciones eléctricas, tanto domésticas como industriales o comerciales, los distintos receptores se conectan todos a la misma tensión, o lo que es lo mismo en conexión paralelo.
Veamos las características de los circuitos y receptores conectados en paralelo.
Conexión Paralelo en Alterna
Podemos ver más abajo dos formas diferentes de representar circuitos en paralelo, como puedes ver a continuación.
Los receptores 1,2,3... pueden ser una resistencia pura (resistivo), una bobina pura (inductivo) o un condesador (capacitivo) o una mezcla de los 3 receptores.
- En los circuitos en paralelo las tensiónes de todos los receptores (o ramas) son la misma.
Imaginemos que en cada rama tenemos solo un receptor, entonces:
- V1 = V2 = V3....
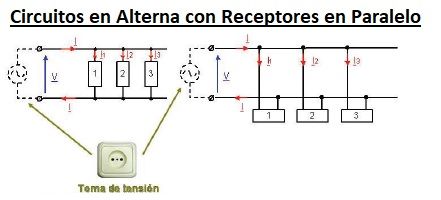
- La intensidad en paralelo es la suma de las intensidades en cada rama, pero OJO, al ser en corriente alterna, será la suma vectorial, ya que la intensidad que atraviesa una resistencia está en fase con la tensión, pero la intensidad que atraviesa una bobina está retrasada 90º y la que atraviesa un condensador adelantada 90º respecto a la tensión (como vimos en circuitos en serie).
Si ponemos todas las tensiones en ángulo 0º, ya que son las mismas en paralelo (VR = VL = VC = Vt = V) y ahora colocamos las intensidades, nos quedaría la intensidad de una resistencia en ángulo 0, la de la bobina retrasada 90º respecto a la intensidad de la resistencia y la intensidad del condensador adelantada 90º respecto a la de la resistencia.
Si lo comparas con las tensiones en serie es justo al contrario.
It = I1 + I2 + I3....Pero OJO ¡¡¡SUMA VECTORIAL DE LAS INTENSIDADES!!!.
El ángulo de desfase de cada intensidad respecto a la tensión, dependerá del tipo de receptor que sea, como ya vimos en serie.
- Los circuitos en paralelo tienen el triángulo de intensidades, los de serie el de tensiones.
- En serie tenemos el triángulo de impedancias, OJO en paralelo NO. En paralelo es muy frecuente trabajar con una nueva magnitud llamada admitancia Y, que es la inversa de la impedancia Y = 1/Z (se mide en Siemens). En paralelo si que tenemos el triángulo de Admitancias (similar al de impedancias en serie). Una vez tenemos la admitancia total podemos obtener la impedancia total, ya que es su inversa.
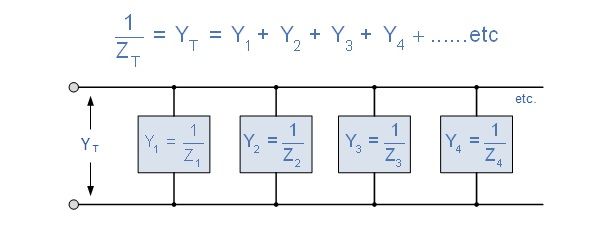
Si Z = V/I la admitancia es 1/Z = Y = I1 /V = I1/V + I2/V + I3/V +.... = (I1 + I2 + I3 +...) / V
De todas formas la impedancia de una resistencia sigue siendo el valor de la resistencia, el de una bobina pura es XL y el de un condensador puro es Xc (como vimos en serie). Todas se miden en ohmios (Ω).
XL = w x L; donde L es el coeficiente de autoinducción medido en Henrios (H) y w = velocidad angular (de la onda de la tensión o intensidad).
Xc = 1 / (w x C); donde C es la capacidad del condensador en faradios.
la velocidad angular (radianes partido por segundo), podemos calcular con la frecuencia de la onda.
w = 2 x pi x f; donde f= frecuencia, y por ejemplo en europa es de 50 hertzios (Hz).
Fíjate los triángulos de impedancias en serie, comparado con los triángulo de admitancias en paralelo para R,L y C.
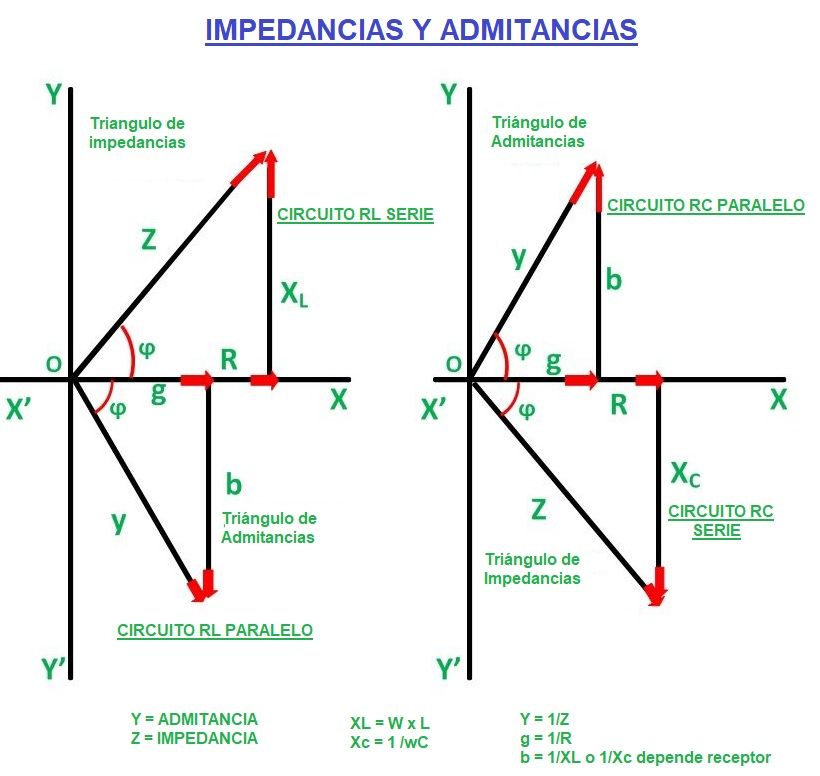
- Al ser la tensión eficaz la misma en cada receptor y una vez que sabemos la impedancia de cada uno, podemos calcular el valor eficaz de la intensidad en cada rama o receptor mediante la ley de ohm.
I1 = V / Z1; I2 = V / Z2; I3 = V/Z3..... Cada una de estas intensidades tiene un ángulo con respecto a la tensión, que viene determinado por el tipo de receptor, por eso OJO, la intensidad total será la suma vectorial de las intensidades en cada receptor.
Pero veamos todo esto con ejemplos concretos que lo entenderemos mejor.
Circuito RL en Paralelo y Corriente Alterna

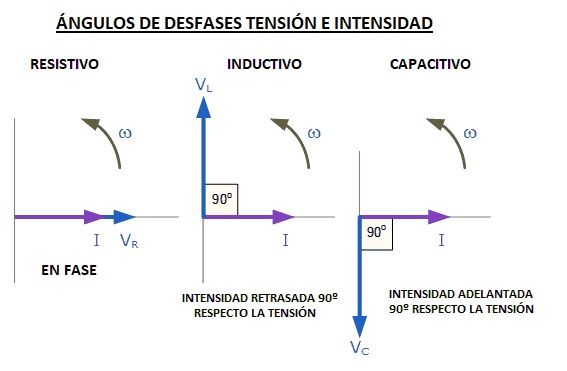
En estos casos podemos obtener el triángulo de intensidades sabiendo que la intensidad de la resistencia pura está en fase con la tensión, y la intensidad de la bobina retrasada 90º respecto a la tensión. De ese triángulo obtenemos las fórmulas que ves arriba por trigonometría. Veamos un ejemplo concreto:
Imagina que conectamos una resistencia de 38,3 ohmios en paralelo con una bobina ideal de Xl = 28,75 ohmios a una fuente de tensión en corriente alterna de 230V de tensión eficaz.
- El receptor de la resistencia pura su impedancia será solo resistiva: Z1 = R = 38,3Ω.
Podemos calcular la intensidad de la resistencia con la ley de ohm: I1 = V /Z1 = 230/38,3 = 6A
La intensidad estará en fase con la tensión por ser resistivo puro, es decir el ángulo de desfase de la de tensión y la I1 será 0º.
- El receptor de la bobina pura su impedancia será solo inductiva (XL = reactancia inductiva) Z2 = Xl = 28,75Ω.
Recuerda que XL = w x L; donde L es la inductáncia medida en henrios.
Podemos calcular la intensidad por la bobina con la ley de ohm: I2 = V / Z2 = 230/28,75= 8A
La intensidad estará retrasada 90º con respecto a la tensión por ser inductivo puro (bobina), es decir el ángulo de desfase de la de tensión y la I2 será -90º.
Si dibujamos el triángulo de intensidades, podemos calcular la intensidad total y el ángulo de desfase total por trigonometria:

Fíjate que la suma de los valores eficaces de las intensidades serían 14A, pero realmente el valor de la intensidad total es de 10A.
Ya tenemos calculado todas las Z, las I y las V. Problema resuelto.
Circuito RC Paralelo
En este caso la intensidad por el condensador estará adelantada 90º respecto a la tensión.
Recuerda Xc = 1/Cw; donde C es la capacidad del condensador medida en faradios.
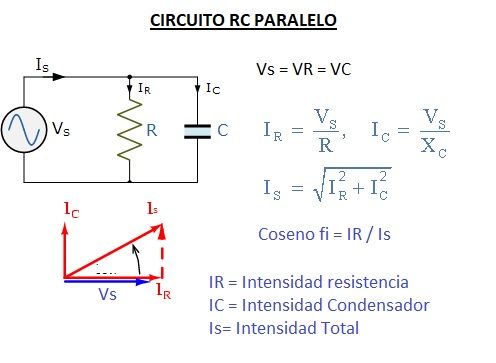
Imagina que R tiene un valor de 30Ω y que el condensador tiene una Xc = 40Ω. La fuente de alimentación en alterna es de 120V. Calculemos:
VR = VL = Vt = 120V
IR = VL/R = 120/30 = 4A
Ic = Vc/Xc = 120/40 = 3A; Xc = reactancia capacitiva.
It = Raiz cuadrada de 4 al cuadrado + 3 al cuadrado= 5 Amperios
Z = V/It = 120/5 = 24Ω
Ya tenemos todas las V, las I y las Z. Problema resuelto.
Circuito RLC en Paralelo
En estos casos el triángulo de intensidadesm, para calcular la intensidad total, será la suma de las 3 intensidades (Resistiva, Inductiva y Capacitiva). Además es mejor trabajar con las admitancias (Y) y luego calcular la impedancia total (Z).
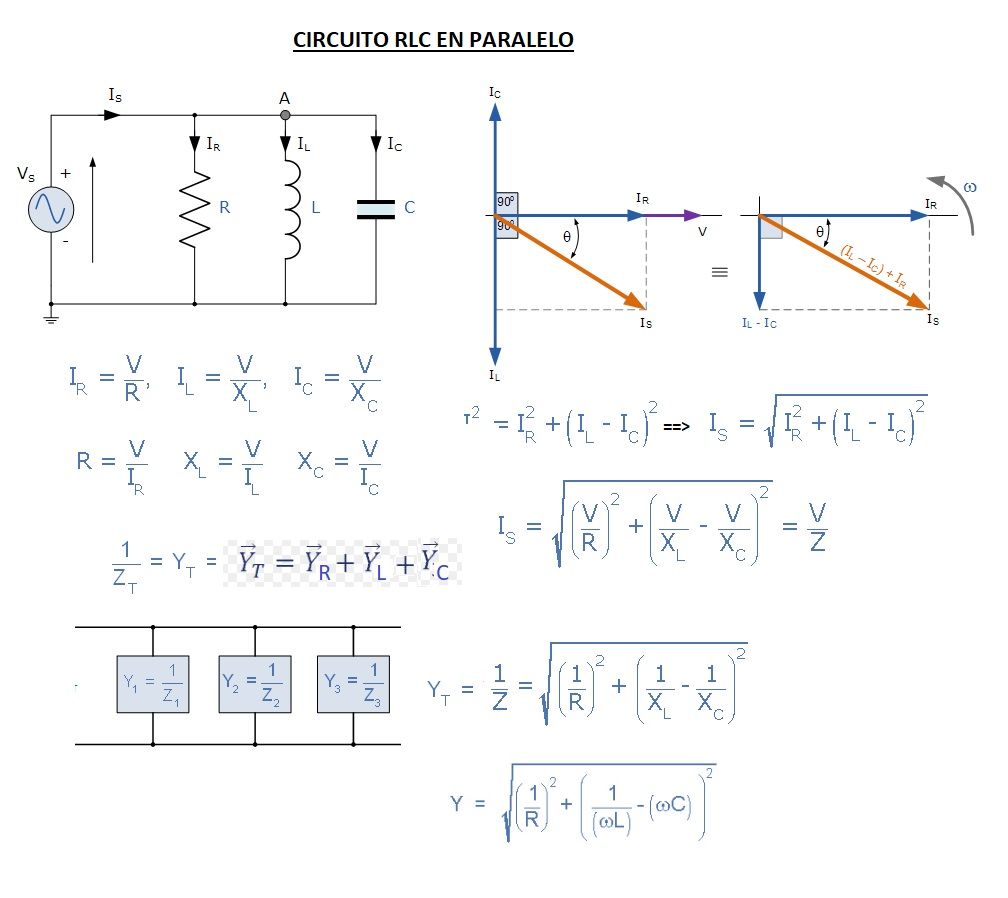
Veamos un ejemplo concreto:
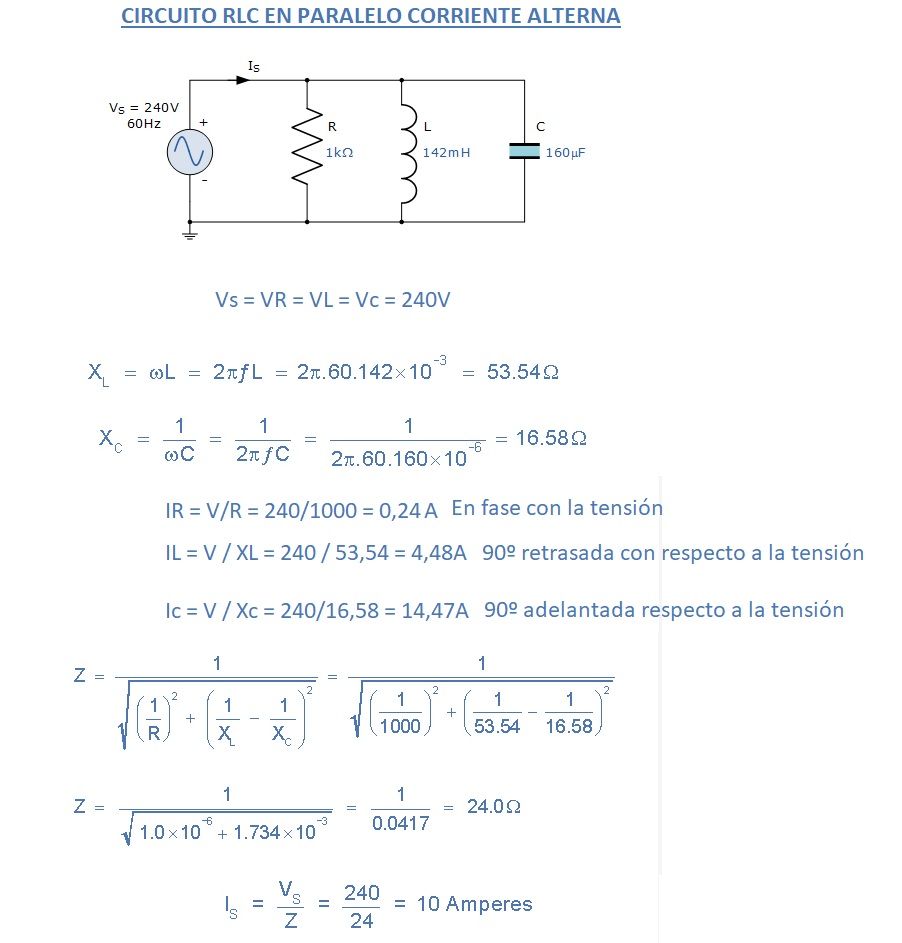
Veamos otro ejercicio RLC paralelo:

Este tipo de ejercicio, al igual que los de serie se pueden resolvar por números complejos.
Circuito Mixtos en Corriente Alterna
Llamaremos circuitos mixtos en corriente alterna a los circuitos que tienen dos o más ramales en paralelo, cada uno de los cuales, a su vez, es un circuito en serie de dos o tres de los elementos posibles. La resolución de este tipo de circuitos se hace resolviendo primero cada ramal por separado (serie), dejando una sola impedancia en cada ramal. Ahora que solo tenemos un receptor (impedancia) en cada rama, resolvemos las ramas en paralelo. Veamos un ejercicio típico mixto en corriente alterna.

Fuente: Areatecnologia