![]()
enguajes de autómatas: Diagramas de Tipo Escalera (LАD)
Un lenguaje de programación es un lenguaje formal diseñado para expresar procesos que pueden ser llevados a cabo por máquinas como puede ser un ordenador. En el caso de los PLCs, los lenguajes de programación para los surgieron junto al mismo tiempo que la aparición del primer PLC, en 1968. Así se explica porque no se utilizaron para este fin lenguajes de programación de alto nivel como Pascal y C y, en su lugar, se emplearon otros lenguajes más simples y fáciles de entender, como podremos ver a continuación.
Fue la tercera parte del estándar IEC 61131, el que consideró estos lenguajes para la programación de los PLCs.
De este modo se definieron los siguientes cinco lenguajes:
• Diagrama de Funciones Secuenciales (SFC) – un lenguaje de bloques de funciones secuenciales;
• Diagrama de Bloques de Funciones (FBD) – un lenguaje de diagramas de bloques secuenciales;
• Diagramas de Tipo Escalera (LАD) – un lenguaje de diagramas de relés (denominado de tipo escalera);
• Texto Estructurado (ST) – un lenguaje de alto nivel como el del tipo de texto estructurado (similar a C y, sobre todo a Pascal);
• Lista de instrucciones (IL o STL) – lenguaje de tipo ensamblador con uso de acumuladores.
En resumen, los lenguajes de programación para PLC son de dos tipos, visuales y escritos. Los visuales (SFC, FBD y LAD) admiten estructurar el programa por medio de símbolos gráficos, similares a los que se han venido utilizando para describir los sistemas de automatización, planos esquemáticos y diagramas de bloques. Sin embargo, los escritos (ST e IL o STL) son listados de sentencias que describen las funciones a ejecutar. Los programadores de PLC poseen formación en múltiples disciplinas y esto determina que exista diversidad de lenguajes. Los programadores de aplicaciones familiarizados con el área industrial prefieren lenguajes visuales, por su parte quienes tienen formación en electrónica e informática optan, inicialmente por los lenguajes escritos.
A continuación se expondrán las características y funciones más básicas de este tipo de lenguajes así como un extracto representativo de cada uno de ellos.
Diagrama de escalera
El diagrama en escalera, también ladder o diagrama ladder, es un lenguaje de programación gráfico muy popular dentro de los autómatas programables debido a que está basado en los esquemas eléctricos de control clásicos. De este modo, con los conocimientos que todo técnico o ingeniero eléctrico posee, es muy fácil adaptarse a la programación en este tipo de lenguaje. En STEP7 se denomina “KOP”.
Ladder es uno de los diferentes lenguajes de programación para los controladores lógicos programables (PLCs) estandarizados con IEC 61131-3. En Ladder, la energía se desplaza de izquierda a derecha en lugar de arriba hacia abajo como en los esquemas eléctricos. En un circuito típico aparecen los contactos en la parte izquierda y una bobina en la parte derecha. La lógica de control que representa dicho circuito puede verse como una inferencia lógica que tiene como antecedente la lógica de los contactos y como concluyente la bobina.
Para programar un autómata con Ladder, además de estar familiarizado con las reglas de los circuitos de conmutación, (también denominada Lógica de Contactos), es necesario conocer cada uno de los elementos de que consta este lenguaje. A continuación se describen de modo general los más comunes (ver Fig. 4.1):
- Contacto normalmente abierto (E1): si la variable asociada E1 vale ‘0’, el contacto permanece abierto, y si vale ‘1’ se cierra.
- Contacto normalmente cerrado (E2): si la variable asociada E1 vale ‘1’, el contacto permanece abierto, y si vale ‘0’ se cierra.
- Salida, bobina o relé (S1): la variable asociada S1 tomará el valor de la variable (o combinación de variables) que esté a su entrada (punto de conexión del lado izquierdo). También se puede enclavar o desenclavar, indicándolo con una S o R como se indica en los casos de S2 y S3.
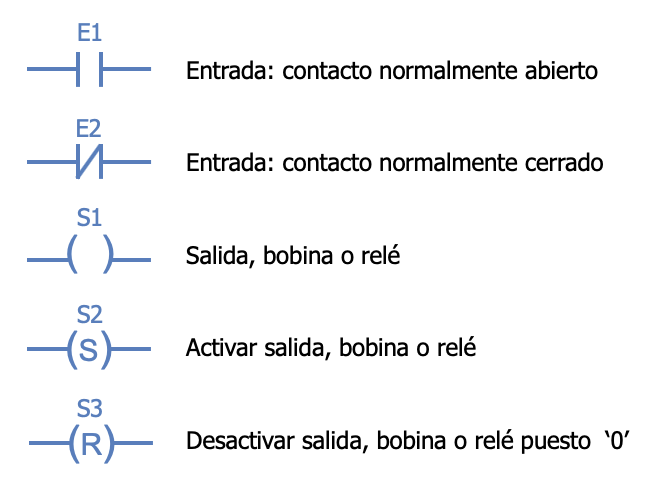
Figura 4.1: Elementos básicos del diagrama de escalera
Nota.- Una bobina normal puede verse como una asignación del valor lógico conectado a su izquierda. Por contra, una bobina de enclavamiento (S / R) se activa de la misma manera que la bobina anterior, pero retiene el valor (‘1’ / ‘0’) aunque el valor lógico conectado a su izquierda pase a ‘0’.
Se pueden implementar funciones lógicas de forma sencilla. Por ejemplo, en la figura siguiente (Fig. 4.2) se implementa un función AND y una OR.
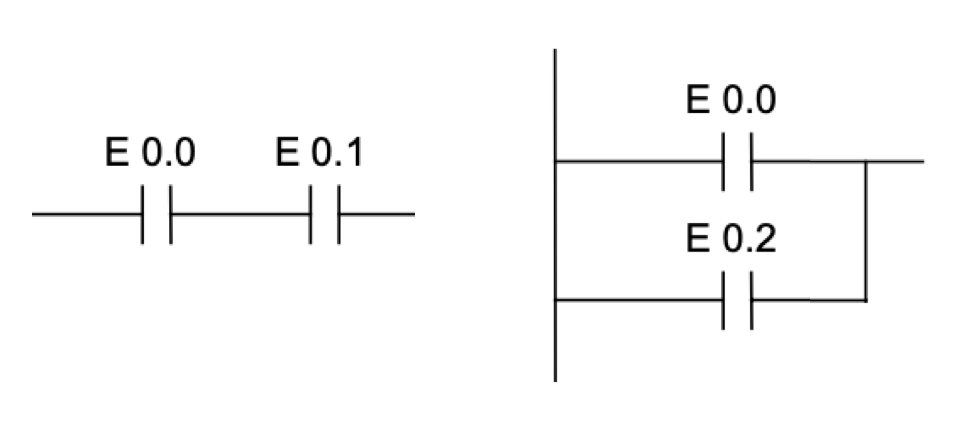
Figura 4.2: Implementación de funciones básicas: AND (izquierda) y OR (derecha)
Más información disponible en (Siemens, 2004a).
Nota.- Si se quiere hacer una simulación de un diagrama KOP de manera interactiva se sugiere el siguiente simulador: https://www.plcfiddle.com/
4.1.1 Ejemplos
El circuito de la Fig. 4.3
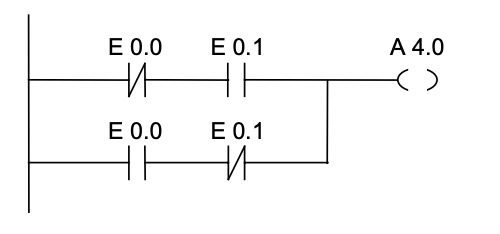
Figura 4.3: Diagrama de escalera: ejemplo 1
equivale a:
A4.0=¯¯¯¯¯¯¯¯¯¯¯E0.0⋅E0.1+E0.0⋅¯¯¯¯¯¯¯¯¯¯¯E0.1=E0.0⊕E0.1A4.0=E0.0¯·E0.1+E0.0·E0.1¯=E0.0⊕E0.1
que corresponde con una puerta XOR.
En el circuito de la Fig. 4.4
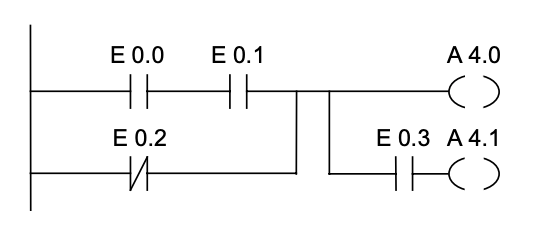
Figura 4.4: Diagrama de escalera: ejemplo 2
la ecuación correspondiente sería la siguiente:
A4.0=E0.0⋅E0.1+¯¯¯¯¯¯¯¯¯¯¯E0.2A4.1=E0.3⋅(E0.0⋅E0.1+¯¯¯¯¯¯¯¯¯¯¯E0.2)(4.1)(4.1)A4.0=E0.0·E0.1+E0.2¯A4.1=E0.3·(E0.0·E0.1+E0.2¯)
En el entorno de desarrollo STEP-7 de SIEMENS, los circuitos se dividen en segmentos, como se muestra en la Fig. 4.5. En este caso se utilizan salidas con activación (S) y desactivación (R).
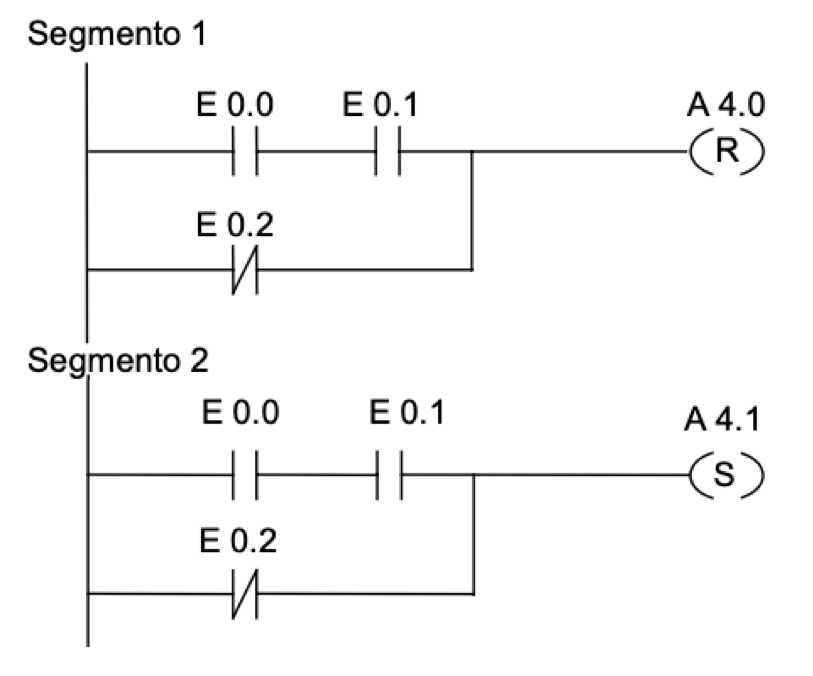
Figura 4.5: Diagrama de escalera: ejemplo 3
Las ecuaciones serían:
A4.0=0 si ((E0.0⋅E0.1)+¯¯¯¯¯¯¯¯¯¯¯E0.2) tiene valor '1' A4.1=1 si ((E0.0⋅E0.1)+¯¯¯¯¯¯¯¯¯¯¯E0.2) tiene valor '1' (4.2)(4.2)A4.0=0 si ((E0.0·E0.1)+E0.2¯) tiene valor '1' A4.1=1 si ((E0.0·E0.1)+E0.2¯) tiene valor '1'
Según lo expuesto anteriormente acerca de las bobinas con enclavamiento, cuando A4.0 toma el valor ‘0’ ya no volverá a tomar el valor ‘1’ (queda desactivada para siempre). De la misma forma, cuando A4.1 toma el valor ‘1’, ya no volverá a tomar el valor ‘0’ (queda activada para siempre).
Referencias
Siemens, Esquema de Contactos (Kop) Para S7-300 Y S7-400, Siemens, 2004a.